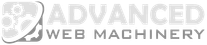JVM JIT optimization techniques - part 2

More measurements of JVM JIT optimization techniques.

Dávid Csákvári

7 mins

In a previous post I wrote a short intro about the high level overview of the JVM optimizations, followed by the results of some measurements, where I crafted small programs to trigger certain optimizations.

JVM JIT optimization techniques

An overview of JVM JIT optimization techniques and fun with measurements.

It gained some attention on some forums, and as I watched the discussions unfold on Reddit or Hacker News, I was truly amazed how many people are enthusiastic about this interesting topic.

I also realized that most of you are more precise than I am. At the time of writing I did not think that anybody will notice or care about the randomly copy-pasted assembly code on the first illustration, but many of you did. :) I hope to have some time in the future to play with JITWatch and the XX:+PrintAssembly flag to be able to correctly address my mistake.

For now, I'd like to continue with the measurements part of the previous post with more optimizations, and share my recent experiences with You.

Back to the Optimization Playground

Code motion

Code motion is a technique to relocate parts of the code from hot paths, attempting to make them execute fewer times.

Expression hoisting is a form of such optimization, where an expression is pulled up in the execution graph, for example by moving the body outside of a loop without changing the semantics of the code. In the following program, the expression related to the result variable is loop invariant, as it's guaranteed to have the same outcome for every loop iteration.

public void hoisting(int x) {
	for (int i = 0; i < 1000; i = i + 1) {
		// Loop invariant computation
		int y = 654;
		int result = x * y;
		
		// Meaningful work with the result
	}
}

The JVM can recognize this and move the calculation out of the loop, making it look like this:

public void manuallyOptimized(int x) {
	int y = 654;
	int result = x * y;
	for (int i = 0; i < 1000; i = i + 1) {
		// Meaningful work with the result
	}
}

Measuring the two code samples above, in terms of speed they perform almost identically due to this optimization. Let's break the loop invariance, by assigning the loop variable to y instead of a constant!

public void noHoisting(int x) {
	for (int i = 0; i < 1000; i = i + 1) {
		// Loop invariant computation - not anymore
		int y = i;
		int result = x * y;
		
		// Meaningful work with the result
	}
}

This is a lot slower than the first version, as all computation has to be executed in every iteration.

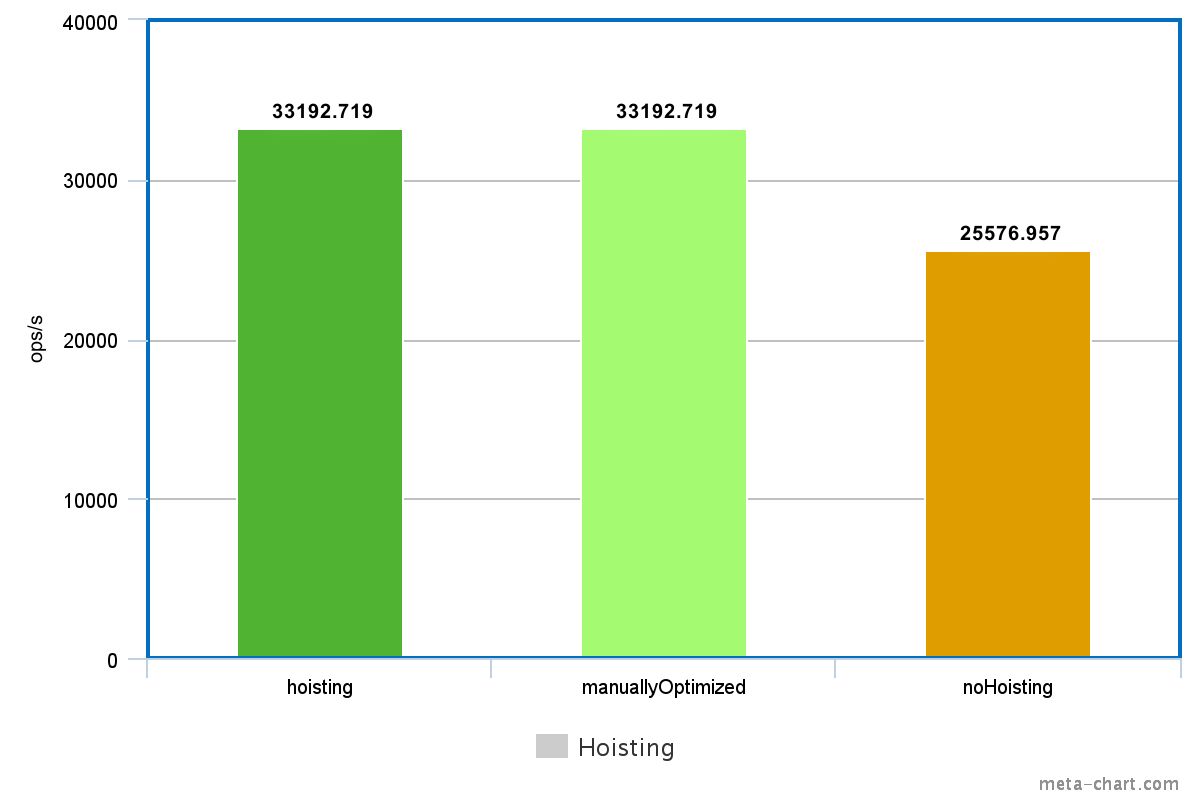
Similarly to hoisting, there is an optimization strategy that moves the affected code down the execution graph, called Expression sinking. This is useful when a precomputed value is not used in all of the subsequent branches. For example, consider the following code:

public void sinking(int i) {
	// Expensive operation
	int result = 543 * i;

	if (i % 2 == 0) {
		// Do some work with the calculated result
	} else {
		// Do some work, but ignore the result.
	}
}

In the else branch the previously calculated result variable is not used. The JVM can recognize this pattern as well, and moves the calculation to the branch where it is needed, making the code above performance-wise similar to the code below:

public void manuallyOptimized(int i) {
	if (i % 2 == 0) {
		// Expensive operation
		int result = 543 * i;

		// Do some work with the calculated result
	} else {
		// Do some work, but ignore the result.
	}
}

Measuring the version where the result is used in both branches shows the speedup potential of this optimization.

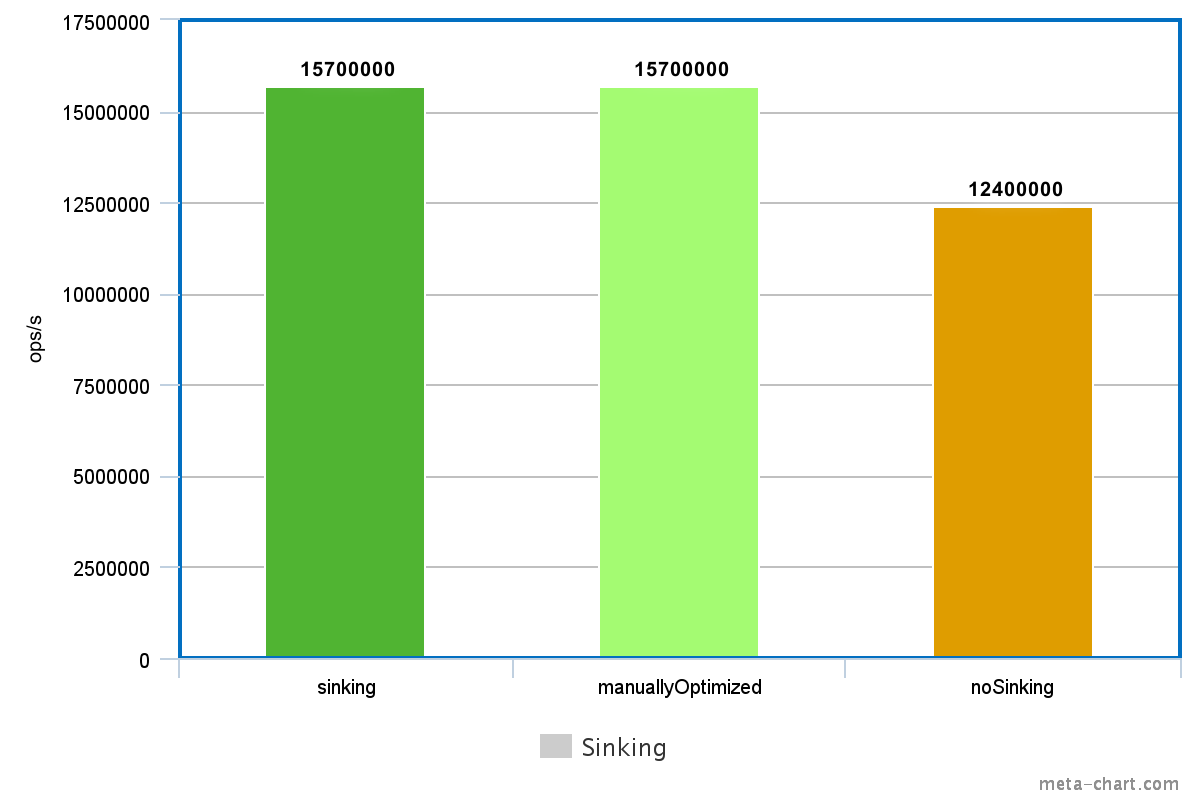
Redundant store elimination

A neat trick the JVM uses is to check if there are any assignments thats result will be overwritten before the stored value is accessed.

int x = i;
int y = 654;
int result = x * y;
result = 5;

In the code above the first assignment to the variable result has no effect on the program semantics, because nobody can see the results of that store operation. In such cases the JVM removes the useless stores, and the unnecessary computations related to them.

So technically it's equivalent with a simple constant assignment, both semantically and performance-wise.

int result = 5;

Measuring the two code snippets turns out that the JVM can indeed optimize this code, resulting in similar performance characteristics. Removing the constant assignment from the first snippet completely changes the outcome of the program, and of course makes the optimization impossible, thus resulting in slower code.

Measurements about Lock redundant store elimination

Loop unswitching

Loop unswitching can be considered a special case of code motion, where the compiler moves a conditional out of the loop, by duplicating it's body.

For example in this case, because the myCondition is loop invariant, it's unnecessary to calculate which branch to take in every iteration.

public void unswitching(int[] array, boolean myCondition) {
	for (int i = 0; i < array.length; i++) {
		if (myCondition) {
			// Some work
		} else {
			// Other work
		}
	}
}

The compiler can transform the code to this, without changing it's meaning:

public void unswitching(int[] array, boolean myCondition) {
	if (myCondition) {
		for (int i = 0; i < array.length; i++) {
			// Some work
		}
	} else {
		for (int i = 0; i < array.length; i++) {
			// Other work
		}
	}
}

The two code snippets above perform similarly, despite the former includes more steps if you decide to execute it step-by-step.

Loop peeling

If there are any special cases need to be handled while looping through an array, it's usually about it's first element.

Loop peeling is a strategy to optimize such cases, by moving the first or the last few iterations outside the loop body, and changing the iteration range of the loop.

Consider this:

int[] array = new int[1000];

for (int i = 0; i < array.length; i++) {
	if (i == 0) {
		// Handling special case
		array[i] = 42;
	} else {
		// Regular operation
		array[i] = i * 2;
	}
}

This optimization (and some subsequent dead code elimination) can transform it to something more performant:

int[] array = new int[1000];

// Handling special case
array[0] = 42;

for (int i = 1; i < array.length; i++) {
	// Regular operation
	array[i] = i * 2;
}

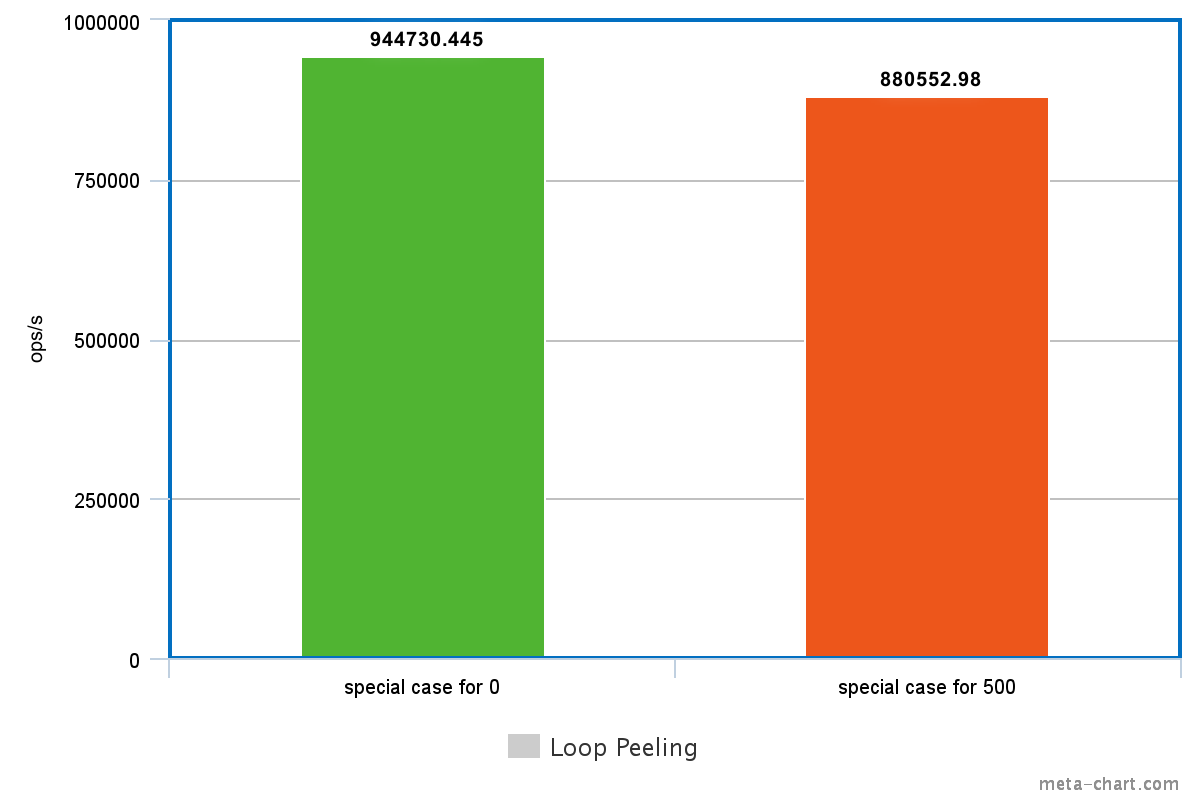
The benefit is, of course, that the special case does not need to be considered in every iteration. The two code snippets perform almost identically thanks to this optimization, but if we change the condition to be something else, the performance gain evaporates.

int[] array = new int[1000];

for (int i = 0; i < array.length; i++) {
	if (i == 500) {
		// Handling special case - in the middle
		array[i] = 42;
	} else {
		// Regular operation
		array[i] = i * 2;
	}
}

Summary

It's really fun to dig into the details of the underlying mechanics, but it's a bit tiresome as well. Although many presentation has long lists about what optimizations are implemented in modern JVMs, for certain ones there are surprisingly low amount of documentation available. Besides, sometimes it's really hard to squeeze the desired behaviour out of the JVM due to it's complexity, so if you are planning to discover them yourself, be sure to be prepared for challenges.

Taking all these advanced and sometimes magical optimizations into account, I think it's important to note that:

You should not optimize for performance unless you have a performance problem that you can measure. What might seem inefficient beforehand, can easily turn out to be performant in practice. Of course this can be true in the opposite direction too.
If you do have a performance problem, then measure, don't guess. Many layers of abstraction divides the source code you see in the IDE from the application running in production, and it's almost impossible to take every one of them into account by looking at just the code.