Running LP and IP optimisation from Java

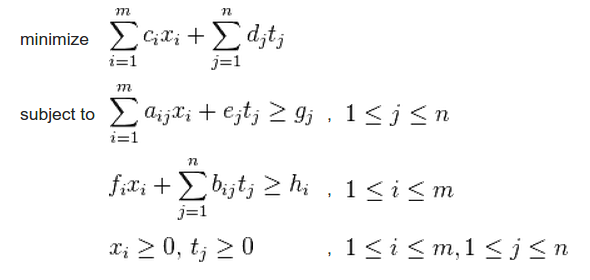
Overview

Linear and Integer programming are essential tools in mathematical optimizations. They can be used to provide an educated answer to a wide range of problems. Although they are not in the mainstream software development, there are some excellent libraries out there. In this post, I'll cover how to run LP and IP computations from Java with ojAlgo.

Adding ojAlgo

Update

This section detailed how to add an extra repository as ojAlgo was missing from Maven Central. Fortunately, it is not true any more, and this part is now obsolete.

Simply add a new dependency to your project:

<dependency>
    <groupId>org.ojalgo</groupId>
    <artifactId>ojalgo</artifactId>
    <version>43.0</version>
</dependency>

The sample problems

First, we need a problem to solve. I've searched a bit and found this, the problem is based on the one described in the 8th slide.

The LP problem

Let's say there are 4 investment funds: The first one is expected to pay $9 for every $6 investment, the second to pay $5 for every $4, the third is to pay $6 for every $5, and the last to pay $4 for every $2. The maximum allowed amount to be bought is capped at $6M, $3M, $5M and $2M, respectively. We have $10M, how much we should buy from each fund?

The problem can be summarized in a table:

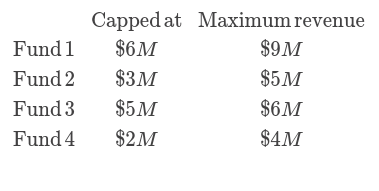And we have $10M to invest.

Formalizing the LP problem

So, we have x₁, x₂, x₃ and x₄, these represents the results we are looking for. And we have the following constraints:

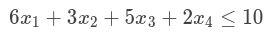
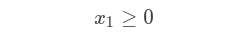
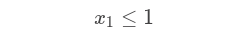
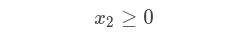
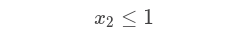
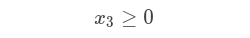
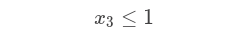
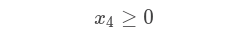
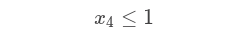
And we have an objective function:

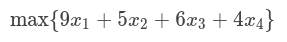
Solving the LP problem in Java

First, we need the four variables with a weight. The weights are the coefficients in the objective function.

Note: I'm using Guava too, as it makes working with collection much more fun.

private static List<Variable> makeVariables(){
	ImmutableList.Builder<Variable> result=ImmutableList.builder();
	result.add(new Variable("X1").weight(9));
	result.add(new Variable("X2").weight(5));
	result.add(new Variable("X3").weight(6));
	result.add(new Variable("X4").weight(4));
	return result.build();
}

And we store them in the variables variable.

Then, we need to construct an ExpressionBasedModel then add the variables:

final ExpressionsBasedModel model = new ExpressionsBasedModel();
for(Variable v:variables){
	model.addVariable(v);
}

Next, we add the constraints. First, the upper constraint:

{
	Expression expression = model.addExpression("C1").upper(10);
	expression.set(variables.get(0), 6);
	expression.set(variables.get(1), 3);
	expression.set(variables.get(2), 5);
	expression.set(variables.get(3), 2);
}

Then that each variable is between 0 and 1 inclusively:

for(Variable v:variables){
	Expression expression = model.addExpression("V_1_"+v.getName()).lower(0);
	expression.set(v, 1);
}

for(Variable v:variables){
	Expression expression = model.addExpression("V_2_"+v.getName()).upper(1);
	expression.set(v, 1);
}

Update: As a shorthand, we can set the constraints directly to the Variable:

for(Variable v:variables){
    v.lower(0).upper(1);
}

Last part is to solve and use the results:

printResult(model.maximise());

...

private static void printResult(Optimisation.Result result){
	System.out.println("X1: "+result.get(0));
	System.out.println("X2: "+result.get(1));
	System.out.println("X3: "+result.get(2));
	System.out.println("X4: "+result.get(3));

	System.out.println("Revenue: " + result.getValue());
}

We can get the individual variables with result.get(..), and the result amount (our sum revenue) with result.getValue()

If we run out program, we get the output:

X1: 0.83333333333300
X2: 1.00000000000000
X3: 0
X4: 1.00000000000000
Revenue: 16.499999999997

The IP problem

Let's rephrase the problem to an IP one! Imagine we have 4 places to build factories. If we build on the first spot, it would cost $6M, but it is expected to produce $9M, the second spot would cost $3M with an expected revenue of $5M, and so on, just like the last example. We have $10M capital, which factories should we build?

Our formalization is exactly the same as for the LP problem, we only have one additional requirement: All the result are integers (in fact they are binary, as we either build the factory or we don't).

In out Java program, making the change is easy, as we just set the variables to be integers with a simple call:

for (Variable v : model.getVariables()) {
	v.setInteger(true);
}

Update: For binary variables, there is a shortcut we can use:

for(Variable v:variables){
    v.binary();
}

This is exactly the same as setting the upper and lower bounds to 1 and 0 respectively along with setting the integer property.

When we run the program, we get the output:

X1: 0
X2: 1.00000000000000
X3: 1.00000000000000
X4: 1.00000000000000

Update

As Optimatika pointed out some best practices when using the API, I've updated the relevant parts. Thanks!

Update #2

As luke777 pointed out, the API changed with v43. I've updated the code samples and the GitHub project. Thanks!