A solution to Codility Kalium

Codility challenge

I recently stumbled on Codility and it's latest open challenge, Kalium. At first glance, it is a very simple problem. It turned out that my initial intuition to approach this problem was plain wrong and it took me about two weeks to come up with a proper solution. In this post I give a detailed overview and my way of thinking behind it.

The challenge in a nutshell is that given a database table with segments on the number line, write an SQL select that results the covered length. For example, for the following data:

The solution would be 3, because the segments are overlapping, and the covered length is 0-3. If one of it would reach to 4, that would modify the solution to 4.

Book

Building GraphQL APIs with AWS AppSync

How to design, implement, and deploy GraphQL-based APIs on the AWS cloud

The first attempt

My first intuition was to simply sum up all the lengths and then subtract all common intervals. The idea might came from how I'd approach this in an imperative language, which SQL is obviously not. The summing part is pretty easy, just a SUM of the difference of the r and l, as they are ordered this way. Getting the intersections is a bit trickier, but not much. The table can be joined with itself on a condition that the joined segments are right to the original one (this sets up an ordering between the segments, so there will be no repetition in the result). The intersection's length is also easily calculated, then summed, finally the solution is ready.

The only problem is that it is wrong. Let's see the following example:

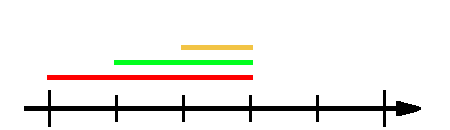
For these segments, we have a total length of 3+2+1=6, and since the join processes all pairs of segments , for red-green, it subtracts 2, for red-gold 1, and for green-gold another one, totaling 4, which yields the final result of 2, which is clearly wrong.

The problem is that we subtracted the gold segment twice. To fix this, we could introduce a 3-way join that adds back all these mistakenly subtracted parts. This would fix this scenario, but if there was a 4-level stack of intervals, it adds back the same interval multiple times, which is also bad. The thinking goes on, we can subtract the all intervals common in 4 segments, add back all 5, subtract all 6, but it will never yield to a general solution.

The second attempt

The main idea is that the problem would be easy if all segments are either fully cover each other or disjoint. If we could transform the original data to this form, then a SELECT DISTINCT and a simple summing would yield the correct result. The good news is that it is not even hard.

First, let's introduce a notion of point of interest: Let's call it a number if it is either the left or the right of a segment.

SELECT    l AS x
FROM      segments
UNION
SELECT    r AS x
FROM      segments

Then the first thing is to define the right points of the new segments. This is a simple join on the pois, where the new right is less than equal to the original one (so it will include the original right too) and greater than the left:

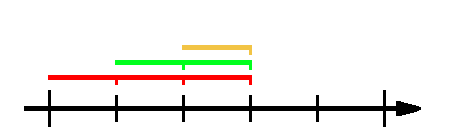
SELECT    x AS r
FROM      segments
JOIN ( SELECT   l AS x
       FROM     segments
       UNION
       SELECT   r AS x
       FROM     segments
     ) AS pois ON x > l AND x <= r

Then when we have all the rights, the lefts will be the greatest poi that is less than the right:

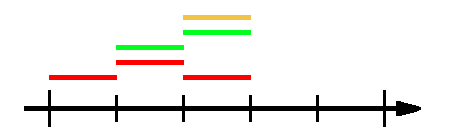
SELECT    MAX(x)
FROM      ( SELECT    l AS x
          FROM      segments
          UNION
          SELECT    r AS x
          FROM      segments
        ) AS pois
WHERE     x < r

Now that we have the new intervals, a simple SELECT DISTINCT and a SUM is all is needed. To handle the edge case where there is no segments at all, an Ifnull is needed.

The complete source for the solution:

SELECT  Ifnull(SUM(r - l), 0)
FROM    ( SELECT DISTINCT
                    r ,
                    ( SELECT    MAX(x)
                      FROM      ( SELECT    l AS x
                                  FROM      segments
                                  UNION
                                  SELECT    r AS x
                                  FROM      segments
                                ) AS pois
                      WHERE     x < r
                    ) AS l
          FROM      ( SELECT    x AS r
                      FROM      segments
                                JOIN ( SELECT   l AS x
                                       FROM     segments
                                       UNION
                                       SELECT   r AS x
                                       FROM     segments
                                     ) AS pois ON x > l
                                                  AND x <= r
                    ) AS rights
        ) AS chopped_segments

(This is a refactored version, for the original blunt one, check this)

This passes all the required tests and scores 100% in the challenge.